Existen muchas librerías en Python que permiten implementar redes neuronales artificiales. En este tutorial, vamos a utilizar la librería scikit-learn, keras y tensorflow para implementar una red neuronal artificial para resolver problemas de clasificación y regresión.
scikit-learnscikit-learn es una librería de Python que permite implementar algoritmos de aprendizaje supervisado y no supervisado. En particular, scikit-learn incluye una clase llamada MLPClassifier que permite implementar redes neuronales artificiales para problemas de clasificación.
En este ejemplo, vamos a utilizar la base de datos iris para entrenar una red neuronal artificial que permita clasificar las flores en tres categorías: setosa, versicolor y virginica.
import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.neural_network import MLPClassifier
# Cargar la base de datos iris
iris = load_iris()
X = iris.data
y = iris.target
print(iris.target_names)
print(iris.feature_names)
print(X.shape)
print(y.shape)['setosa' 'versicolor' 'virginica']
['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
(150, 4)
(150,)Implementamos la red neuronal artificial y la entrenamos con la base de datos iris.
# Dividir la base de datos en entrenamiento y prueba
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Crear la red neuronal artificial
clf = MLPClassifier(hidden_layer_sizes=(10, 10), max_iter=1000, random_state=42,
activation='relu', solver='sgd', learning_rate='adaptive',
learning_rate_init=0.001)
# Entrenar la red neuronal artificial
clf.fit(X_train, y_train)
# Evaluar la red neuronal artificial
score = clf.score(X_test, y_test)
print(score)0.9333333333333333La clase MLPClassifier tiene varios parámetros que permiten configurar la red neuronal artificial. En este ejemplo, utilizamos los siguientes parámetros:
hidden_layer_sizes: Número de neuronas en cada capa oculta.max_iter: Número máximo de iteraciones para entrenar la red neuronal artificial.random_state: Semilla para la generación de números aleatorios.solver: Algoritmo de optimización para entrenar la red neuronal artificial.activation: Función de activación para las neuronas en las capas ocultas.learning_rate: Tasa de aprendizaje para actualizar los pesos de la red neuronal artificial.learning_rate_init: Tasa de aprendizaje inicial para actualizar los pesos de la red neuronal artificial.El método score permite evaluar la precisión de la red neuronal artificial en la base de datos de prueba.
Podemos obtener las predicciones de la red neuronal artificial para la base de datos de prueba.
[1 0 2 1 1 0 1 2 2 1 2 0 0 0 0 1 2 1 1 2 0 2 0 2 1 2 2 2 0 0]Para evaluar la red neuronal artificial, podemos calcular la matriz de confusión.
[[10 0 0]
[ 0 8 1]
[ 0 1 10]]Podemos visualizar la matriz de confusión utilizando la librería seaborn.
Con este mapa de color podemos visualizar la matriz de confusión. Las filas representan las categorías reales y las columnas representan las categorías predichas. Los valores en la diagonal principal representan las predicciones correctas y esperamos que un buen modelo tenga valores altos en la diagonal principal.
POdemos usar el área bajo la curva ROC para evaluar la red neuronal artificial.
0.9966414352379265Aquí el parámetro multi_class se refiere a la estrategia de codificación de clases. En este caso, utilizamos ovr que significa “one-vs-rest”, que evalúa cada clase en comparación con el resto de las clases y es sensible a datos desequilibrados.
Entre más cercano a 1 sea el valor del área bajo la curva ROC, mejor será el modelo, ya que significa que el modelo es capaz de distinguir entre las diferentes clases.
PyTorchPyTorch es una librería de Python que permite implementar redes neuronales artificiales de manera eficiente. En particular, PyTorch incluye una clase llamada nn.Module que permite definir la arquitectura de la red neuronal artificial.
Para utilizar PyTorch, primero debemos instalar la librería, el comando que recomienda la página de PyTorch es el siguiente para Windows y sin el uso de GPU.
En PyTorch, los datos se almacenan en tensores, que son arreglos multidimensionales similares a los arreglos de NumPy. Podemos crear tensores en PyTorch de la siguiente manera.
tensor([[0., 0., 0.],
[0., 0., 0.]])Podemos crear tensores a partir de arreglos de NumPy.
tensor([[1, 2, 3],
[4, 5, 6]])Los tensores pueden ser de diferentes tipos de datos, como float32, int64, bool, etc.
tensor([[1, 2, 3],
[4, 5, 6]])
tensor([[ True, False],
[False, True]])
tensor([[1., 2.],
[3., 4.]])Podemos tener tensores de cualquier dimensión.
Podemos realizar operaciones matemáticas con tensores en PyTorch.
# Crear dos tensores
x = torch.tensor([[1, 2], [3, 4]], dtype=torch.float32)
y = torch.tensor([[5, 6], [7, 8]], dtype=torch.float32)
# Sumar los tensores
z = x + y
print(z)
# Multiplicar los tensores
z = x * y
print(z)
# Multiplicar un tensor por un escalar
z = 2 * x
print(z)
# Calcular la transpuesta de un tensor
z = x.t()
print(z)
# Calcular el producto punto de dos tensores
z = torch.dot(x.view(-1), y.view(-1))
print(z)
# Calcular el producto matricial de dos tensores
z = torch.mm(x, y)
print(z)
# Calcular la inversa de un tensor
z = torch.inverse(x)
print(z)
# Calcular la norma de un tensor
z = torch.norm(x)
print(z)
# Calcular la media de un tensor
z = torch.mean(x)
print(z)
# Calcular la desviación estándar de un tensor
z = torch.std(x)
print(z)tensor([[ 6., 8.],
[10., 12.]])
tensor([[ 5., 12.],
[21., 32.]])
tensor([[2., 4.],
[6., 8.]])
tensor([[1., 3.],
[2., 4.]])
tensor(70.)
tensor([[19., 22.],
[43., 50.]])
tensor([[-2.0000, 1.0000],
[ 1.5000, -0.5000]])
tensor(5.4772)
tensor(2.5000)
tensor(1.2910)Los tensores en PyTorch tienen varios métodos útiles.
# Crear un tensor de 3 dimensiones
x = torch.tensor([[[1, 2], [3, 4]], [[5, 6], [7, 8]]])
# Obtener la forma del tensor
print(f"Shape: {x.shape}")
# Obtener el número de elementos en el tensor
print(f"Size: {x.size()}")
# Obtener el tipo de datos del tensor
print(f"Data type: {x.dtype}")
# Obtener el dispositivo en el que se almacena el tensor
print(f"Device: {x.device}")
# Obtener el número de dimensiones del tensor
print(f"Number of dimensions: {x.dim()}")
# Obtener el número de elementos en una dimensión específica
print(f"Number of elements in the first dimension: {x.size(0)}")
# Obtener el elemento en una posición específica
print(f"Element at position (0, 1, 1): {x[0, 1, 1]}")
# Obtener un subtensor
print(f"Subtensor: {x[0, :, :]}")
# Cambiar la forma del tensor
print(f"Reshape: {x.view(2, 4)}")
# Aplanar el tensor
print(f"Flatten: {x.view(-1)}")
# Concatenar tensores
y = torch.tensor([[[9, 10], [11, 12]], [[13, 14], [15, 16]]])
z = torch.cat((x, y), dim=0)
print(z)
# Dividir un tensor
z1, z2 = torch.chunk(z, 2, dim=0)
print(f"z1: {z1}")
print(f"z2: {z2}")
# Calcular la suma acumulada de un tensor
z = torch.cumsum(x, dim=0)
print(f"Cumulative sum: {z}")Shape: torch.Size([2, 2, 2])
Size: torch.Size([2, 2, 2])
Data type: torch.int64
Device: cpu
Number of dimensions: 3
Number of elements in the first dimension: 2
Element at position (0, 1, 1): 4
Subtensor: tensor([[1, 2],
[3, 4]])
Reshape: tensor([[1, 2, 3, 4],
[5, 6, 7, 8]])
Flatten: tensor([1, 2, 3, 4, 5, 6, 7, 8])
tensor([[[ 1, 2],
[ 3, 4]],
[[ 5, 6],
[ 7, 8]],
[[ 9, 10],
[11, 12]],
[[13, 14],
[15, 16]]])
z1: tensor([[[1, 2],
[3, 4]],
[[5, 6],
[7, 8]]])
z2: tensor([[[ 9, 10],
[11, 12]],
[[13, 14],
[15, 16]]])
Cumulative sum: tensor([[[ 1, 2],
[ 3, 4]],
[[ 6, 8],
[10, 12]]])Veamos las distintas partes de una red neuronal artificial en PyTorch.
En este ejemplo, vamos a utilizar la base de datos iris para entrenar una red neuronal artificial que permita clasificar las flores en tres categorías: setosa, versicolor y virginica.
import torch
import torch.nn as nn
# Crear la red neuronal artificial
class MLP(nn.Module):
def __init__(self):
super(MLP, self).__init__()
self.fc1 = nn.Linear(4, 10)
self.fc2 = nn.Linear(10, 10)
self.fc3 = nn.Linear(10, 3)
self.relu = nn.ReLU()
self.softmax = nn.Softmax(dim=1)
def forward(self, x):
x = self.relu(self.fc1(x))
x = self.relu(self.fc2(x))
x = self.fc3(x)
x = self.softmax(x)
return x
model = MLP()
print(model)MLP(
(fc1): Linear(in_features=4, out_features=10, bias=True)
(fc2): Linear(in_features=10, out_features=10, bias=True)
(fc3): Linear(in_features=10, out_features=3, bias=True)
(relu): ReLU()
(softmax): Softmax(dim=1)
)Para crear la red neuronal artificial, definimos una clase llamada MLP que hereda de nn.Module. En el método __init__, definimos las capas de la red neuronal artificial y las funciones de activación. En el método forward, definimos la arquitectura de la red neuronal artificial.
Dentro del método __init__, usamos la función super para inicializar la clase base nn.Module. Luego, definimos las capas de la red neuronal artificial utilizando la clase nn.Linear que representa una capa de neuronas completamente conectada. En este caso, definimos tres capas de neuronas con 4, 10 y 3 neuronas respectivamente.
También definimos las funciones de activación nn.ReLU y nn.Softmax para las capas ocultas y de salida respectivamente. La función de activación ReLU se utiliza para introducir no linealidades en la red neuronal artificial, mientras que la función de activación Softmax se utiliza para obtener probabilidades de las clases y recive como argumento la dimensión en la que se calcula el softmax.
En el método forward, definimos la arquitectura de la red neuronal artificial. Primero aplicamos la capa fc1 seguida de la función de activación ReLU. Luego aplicamos la capa fc2 seguida de la función de activación ReLU. Finalmente aplicamos la capa fc3 seguida de la función de activación Softmax.
La función Linear aplicará una transformación lineal a los datos de entrada: \(y = xA^T + b\), donde \(x\) es la entrada, \(A\) es la matriz de pesos y \(b\) es el vector de sesgos.
Es importante que las neuronas entre capas tengan la misma cantidad de neuronas que la capa anterior y la capa siguiente. En este caso, la capa de entrada tiene 4 neuronas, la capa oculta tiene 10 neuronas y la capa de salida tiene 3 neuronas.
Vamos a usar la base de datos iris para ver que resultados obtenemos.
import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
# Cargar la base de datos iris
iris = load_iris()
X = iris.data
y = iris.target
model = MLP()
# Convertir los datos a tensores de PyTorch
X = torch.tensor(X, dtype=torch.float32)
y = torch.tensor(y, dtype=torch.long)
print(X.shape)
print(y.shape)
# Obtener las predicciones de la red neuronal artificial
y_pred = model(X)
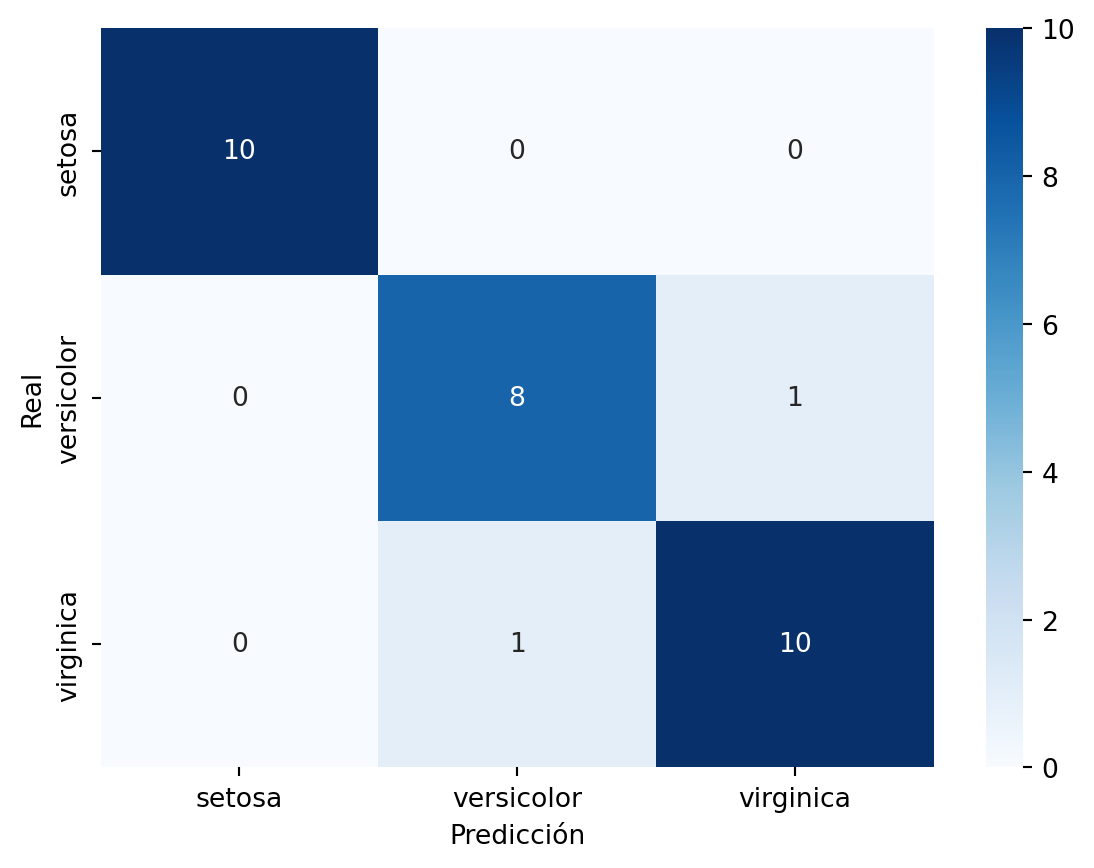
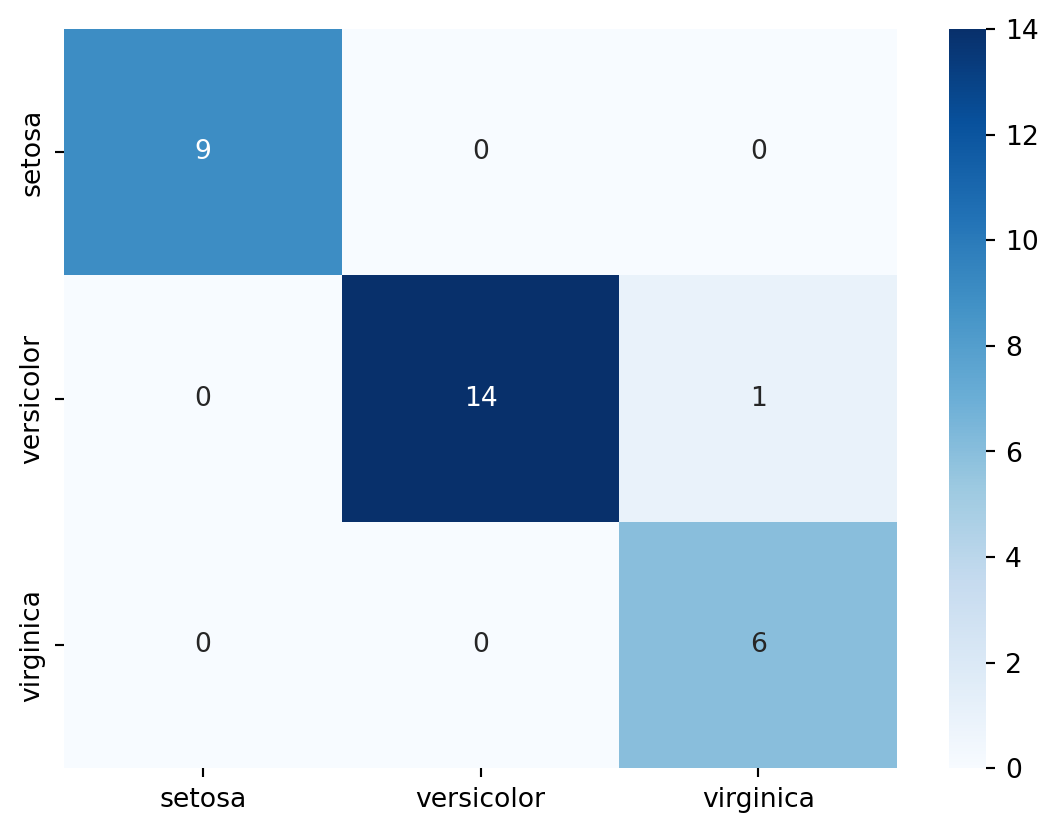
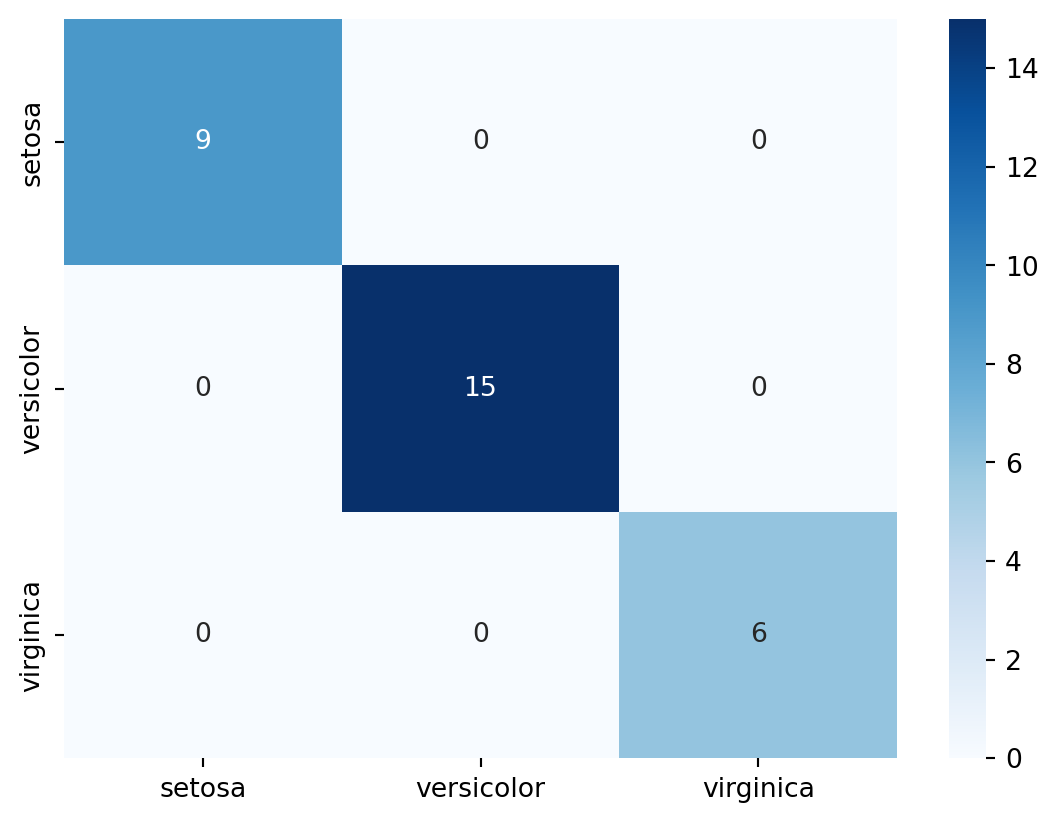
print(y_pred)torch.Size([150, 4])
torch.Size([150])
tensor([[0.3815, 0.2707, 0.3478],
[0.3707, 0.2763, 0.3529],
[0.3767, 0.2748, 0.3485],
[0.3761, 0.2767, 0.3472],
[0.3848, 0.2700, 0.3452],
[0.3857, 0.2675, 0.3468],
[0.3805, 0.2740, 0.3455],
[0.3804, 0.2723, 0.3473],
[0.3722, 0.2792, 0.3486],
[0.3762, 0.2751, 0.3487],
[0.3846, 0.2679, 0.3474],
[0.3825, 0.2732, 0.3442],
[0.3740, 0.2762, 0.3498],
[0.3763, 0.2772, 0.3465],
[0.3872, 0.2628, 0.3499],
[0.3947, 0.2610, 0.3442],
[0.3835, 0.2665, 0.3500],
[0.3790, 0.2712, 0.3498],
[0.3833, 0.2669, 0.3498],
[0.3871, 0.2685, 0.3445],
[0.3782, 0.2714, 0.3503],
[0.3820, 0.2700, 0.3479],
[0.3859, 0.2704, 0.3438],
[0.3707, 0.2750, 0.3542],
[0.3841, 0.2740, 0.3418],
[0.3710, 0.2765, 0.3525],
[0.3759, 0.2736, 0.3505],
[0.3813, 0.2706, 0.3481],
[0.3782, 0.2713, 0.3505],
[0.3783, 0.2756, 0.3461],
[0.3751, 0.2763, 0.3487],
[0.3722, 0.2719, 0.3559],
[0.3988, 0.2640, 0.3371],
[0.3958, 0.2623, 0.3418],
[0.3737, 0.2756, 0.3506],
[0.3738, 0.2735, 0.3527],
[0.3777, 0.2690, 0.3532],
[0.3881, 0.2698, 0.3420],
[0.3741, 0.2779, 0.3480],
[0.3796, 0.2719, 0.3485],
[0.3793, 0.2713, 0.3494],
[0.3538, 0.2849, 0.3613],
[0.3791, 0.2759, 0.3450],
[0.3735, 0.2737, 0.3529],
[0.3867, 0.2701, 0.3432],
[0.3691, 0.2772, 0.3537],
[0.3901, 0.2682, 0.3417],
[0.3781, 0.2754, 0.3465],
[0.3854, 0.2683, 0.3463],
[0.3773, 0.2730, 0.3496],
[0.3250, 0.2925, 0.3825],
[0.3263, 0.2936, 0.3801],
[0.3203, 0.2957, 0.3840],
[0.3146, 0.3016, 0.3837],
[0.3154, 0.3000, 0.3847],
[0.3272, 0.2929, 0.3800],
[0.3270, 0.2936, 0.3794],
[0.3322, 0.2924, 0.3754],
[0.3230, 0.2938, 0.3832],
[0.3244, 0.2970, 0.3785],
[0.3196, 0.2988, 0.3816],
[0.3244, 0.2961, 0.3795],
[0.3173, 0.2974, 0.3853],
[0.3239, 0.2944, 0.3816],
[0.3294, 0.2935, 0.3772],
[0.3242, 0.2940, 0.3818],
[0.3271, 0.2943, 0.3786],
[0.3342, 0.2883, 0.3776],
[0.3119, 0.3071, 0.3809],
[0.3256, 0.2940, 0.3803],
[0.3213, 0.2986, 0.3800],
[0.3233, 0.2955, 0.3811],
[0.3136, 0.3026, 0.3839],
[0.3275, 0.2911, 0.3814],
[0.3241, 0.2940, 0.3818],
[0.3223, 0.2953, 0.3824],
[0.3160, 0.2979, 0.3861],
[0.3157, 0.3008, 0.3834],
[0.3213, 0.2972, 0.3815],
[0.3307, 0.2913, 0.3780],
[0.3234, 0.2956, 0.3810],
[0.3272, 0.2933, 0.3795],
[0.3259, 0.2940, 0.3801],
[0.3147, 0.3010, 0.3843],
[0.3287, 0.2937, 0.3776],
[0.3317, 0.2916, 0.3767],
[0.3216, 0.2956, 0.3828],
[0.3131, 0.3023, 0.3846],
[0.3331, 0.2904, 0.3765],
[0.3200, 0.2984, 0.3816],
[0.3268, 0.2932, 0.3801],
[0.3265, 0.2931, 0.3804],
[0.3234, 0.2953, 0.3813],
[0.3282, 0.2944, 0.3774],
[0.3248, 0.2950, 0.3802],
[0.3364, 0.2879, 0.3757],
[0.3294, 0.2921, 0.3784],
[0.3257, 0.2934, 0.3809],
[0.3285, 0.2949, 0.3766],
[0.3266, 0.2940, 0.3794],
[0.3149, 0.3109, 0.3742],
[0.3139, 0.3066, 0.3794],
[0.3139, 0.3074, 0.3787],
[0.3150, 0.3018, 0.3833],
[0.3141, 0.3085, 0.3774],
[0.3133, 0.3066, 0.3801],
[0.3142, 0.3049, 0.3809],
[0.3139, 0.3020, 0.3841],
[0.3121, 0.3071, 0.3808],
[0.3163, 0.3076, 0.3762],
[0.3162, 0.3037, 0.3801],
[0.3134, 0.3073, 0.3793],
[0.3143, 0.3078, 0.3779],
[0.3125, 0.3112, 0.3763],
[0.3129, 0.3155, 0.3716],
[0.3153, 0.3091, 0.3757],
[0.3154, 0.3012, 0.3834],
[0.3179, 0.2985, 0.3836],
[0.3100, 0.3151, 0.3749],
[0.3120, 0.3055, 0.3826],
[0.3147, 0.3090, 0.3762],
[0.3145, 0.3075, 0.3780],
[0.3123, 0.3070, 0.3807],
[0.3139, 0.3061, 0.3800],
[0.3162, 0.3033, 0.3805],
[0.3160, 0.2988, 0.3852],
[0.3146, 0.3049, 0.3805],
[0.3159, 0.3019, 0.3821],
[0.3133, 0.3093, 0.3774],
[0.3154, 0.2978, 0.3868],
[0.3130, 0.3059, 0.3811],
[0.3184, 0.2957, 0.3859],
[0.3130, 0.3113, 0.3757],
[0.3172, 0.2980, 0.3848],
[0.3172, 0.2967, 0.3861],
[0.3127, 0.3121, 0.3752],
[0.3162, 0.3076, 0.3762],
[0.3161, 0.2998, 0.3841],
[0.3160, 0.3020, 0.3820],
[0.3148, 0.3070, 0.3782],
[0.3140, 0.3122, 0.3739],
[0.3143, 0.3118, 0.3739],
[0.3139, 0.3066, 0.3794],
[0.3148, 0.3083, 0.3769],
[0.3149, 0.3114, 0.3737],
[0.3138, 0.3124, 0.3738],
[0.3123, 0.3104, 0.3773],
[0.3149, 0.3060, 0.3791],
[0.3167, 0.3059, 0.3775],
[0.3164, 0.3010, 0.3826]], grad_fn=<SoftmaxBackward0>)Que nos regresa un tensor con las probabilidades de cada clase para cada observación. Para obtener la clase predicha, podemos usar la función argmax de PyTorch.
tensor([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 0, 0, 0, 0, 0, 0,
0, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2])En PyTorch, las funciones de activación se pueden utilizar como capas en una red neuronal artificial. Las funciones de activación más comunes son ReLU, Sigmoid y Softmax.
import torch
# Crear un tensor de entrada
x = torch.tensor([[1.0, -1.0], [-1.0, 1.0]])
# Función de activación ReLU
relu = torch.nn.ReLU()
y = relu(x)
print(f"ReLU: {y}")
# Función de activación Sigmoid
sigmoid = torch.nn.Sigmoid()
y = sigmoid(x)
print(f"Sigmoid: {y}")
# Función de activación Softmax
softmax = torch.nn.Softmax(dim=1)
y = softmax(x)
print(f"Softmax: {y}")
# Función de activación Tanh
tanh = torch.nn.Tanh()
y = tanh(x)
print(f"Tanh: {y}")
# Función de activación LeakyReLU
leaky_relu = torch.nn.LeakyReLU(negative_slope=0.01)
y = leaky_relu(x)
print(f"LeakyReLU: {y}")ReLU: tensor([[1., 0.],
[0., 1.]])
Sigmoid: tensor([[0.7311, 0.2689],
[0.2689, 0.7311]])
Softmax: tensor([[0.8808, 0.1192],
[0.1192, 0.8808]])
Tanh: tensor([[ 0.7616, -0.7616],
[-0.7616, 0.7616]])
LeakyReLU: tensor([[ 1.0000, -0.0100],
[-0.0100, 1.0000]])Para entrenar la red neuronal artificial, primero debemos definir una función de pérdida y un optimizador.
La función de pérdida mide la diferencia entre las predicciones de la red neuronal artificial y las etiquetas reales. Existen diversas funciones de pérdida para problemas de clasificación y regresión.
nn.CrossEntropyLoss: Utilizada para problemas de clasificación multiclase.nn.BCELoss: Utilizada para problemas de clasificación binaria.nn.NLLLoss: Utilizada para problemas de clasificación multiclase con salida logarítmica.nn.MSELoss: Utilizada para problemas de regresión de mínimos cuadrados.nn.L1Loss: Utilizada para problemas de regresión de mínimos absolutos.nn.SmoothL1Loss: Utilizada para problemas de regresión de mínimos suavizados.tensor(0.7694)Nos regresa el error de la red neuronal. Para minimizar la función de pérdida, utilizamos un optimizador.
El optimizador ajusta los pesos de la red neuronal artificial para minimizar la función de pérdida. Existen diversos optimizadores que se pueden utilizar para entrenar una red neuronal artificial.
torch.optim.SGD: Descenso de gradiente estocástico.torch.optim.Adam: Algoritmo de optimización basado en el método de Adam.torch.optim.RMSprop: Algoritmo de optimización basado en el método de RMSprop.Cadad optimizador tiene sus propios hiperparámetros que se pueden ajustar para mejorar el rendimiento de la red neuronal artificial.
En este caso, utilizamos el optimizador SGD con una tasa de aprendizaje de 0.01. Primero, llamamos al método zero_grad para restablecer los gradientes de los pesos de la red neuronal artificial. Luego, llamamos al método backward para calcular los gradientes de la función de pérdida con respecto a los pesos. Finalmente, llamamos al método step para actualizar los pesos de la red neuronal artificial utilizando el algoritmo de optimización.
Estos pasos se repiten varias veces para entrenar la red neuronal artificial en un conjunto de datos.
Para entrenar una red neuronal artificial, primero debemos preparar los datos en tensores de PyTorch.
import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
# Cargar la base de datos iris
iris = load_iris()
X = iris.data
y = iris.target
# Dividir la base de datos en entrenamiento y prueba
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1014)
# Convertir los datos a tensores de PyTorch
X_train = torch.tensor(X_train, dtype=torch.float32)
X_test = torch.tensor(X_test, dtype=torch.float32)
y_train = torch.tensor(y_train, dtype=torch.long)
y_test = torch.tensor(y_test, dtype=torch.long)
print(X_train.shape)
print(X_test.shape)
print(y_train.shape)
print(y_test.shape)torch.Size([120, 4])
torch.Size([30, 4])
torch.Size([120])
torch.Size([30])Los datos tipo torch.long es equivalente a int64 en NumPy y se utiliza para representar las etiquetas de las clases.
Vamos a definir una red neuronal de 2 capas ocultas con 4 neuronas cada capa y una capa de salida con 3 neuronas.
class NeuralNetwork(nn.Module):
def __init__(self):
super(NeuralNetwork, self).__init__()
self.fc1 = nn.Linear(4, 4)
self.fc2 = nn.Linear(4, 4)
self.fc3 = nn.Linear(4, 3)
self.relu = nn.ReLU()
self.softmax = nn.Softmax(dim=1)
def forward(self, x):
x = self.relu(self.fc1(x))
x = self.relu(self.fc2(x))
x = self.fc3(x)
x = self.softmax(x)
return x
def predict(self, x):
with torch.no_grad():
y = self.forward(x)
return torch.argmax(y, dim=1)
model = NeuralNetwork()
print(model)NeuralNetwork(
(fc1): Linear(in_features=4, out_features=4, bias=True)
(fc2): Linear(in_features=4, out_features=4, bias=True)
(fc3): Linear(in_features=4, out_features=3, bias=True)
(relu): ReLU()
(softmax): Softmax(dim=1)
)Ahora creemos una función para entrenar la red neuronal.
Ahora vamos a entrenar la red neuronal.
Epoch 50/1000, Loss: 1.0754790306091309
Epoch 100/1000, Loss: 1.07102370262146
Epoch 150/1000, Loss: 1.067678689956665
Epoch 200/1000, Loss: 1.0643763542175293
Epoch 250/1000, Loss: 1.0608757734298706
Epoch 300/1000, Loss: 1.0570424795150757
Epoch 350/1000, Loss: 1.052795648574829
Epoch 400/1000, Loss: 1.0484215021133423
Epoch 450/1000, Loss: 1.043760895729065
Epoch 500/1000, Loss: 1.0385349988937378
Epoch 550/1000, Loss: 1.0325710773468018
Epoch 600/1000, Loss: 1.0256762504577637
Epoch 650/1000, Loss: 1.0176128149032593
Epoch 700/1000, Loss: 1.0081112384796143
Epoch 750/1000, Loss: 0.9968506693840027
Epoch 800/1000, Loss: 0.9835156798362732
Epoch 850/1000, Loss: 0.9678962826728821
Epoch 900/1000, Loss: 0.9499657154083252
Epoch 950/1000, Loss: 0.9237939119338989
Epoch 1000/1000, Loss: 0.9007318615913391Finalmente, vamos a evaluar la red neuronal en la base de datos de prueba.
tensor([2, 2, 2, 0, 2, 0, 2, 0, 2, 2, 0, 2, 0, 2, 2, 2, 0, 0, 2, 2, 2, 2, 2, 2,
0, 2, 2, 0, 2, 2])Calculamos la precisión de la red neuronal.
Accuracy: 0.5Como vemos, la red tiene un precisión muy baja, esto se debe a que la red neuronal es muy compleja para el problema que estamos tratando de resolver. Dismunuyamos la complejidad de la red neuronal.
class NeuralNetwork(nn.Module):
def __init__(self):
super(NeuralNetwork, self).__init__()
self.fc1 = nn.Linear(4, 2)
self.fc2 = nn.Linear(2, 3)
self.relu = nn.ReLU()
self.softmax = nn.Softmax(dim=1)
def forward(self, x):
x = self.relu(self.fc1(x))
x = self.fc2(x)
x = self.softmax(x)
return x
def predict(self, x):
with torch.no_grad():
y = self.forward(x)
return torch.argmax(y, dim=1)
model = NeuralNetwork()
print(model)NeuralNetwork(
(fc1): Linear(in_features=4, out_features=2, bias=True)
(fc2): Linear(in_features=2, out_features=3, bias=True)
(relu): ReLU()
(softmax): Softmax(dim=1)
)Entrenamos la red neuronal.
Epoch 50/1500, Loss: 1.0786900520324707
Epoch 100/1500, Loss: 1.0306339263916016
Epoch 150/1500, Loss: 0.9199546575546265
Epoch 200/1500, Loss: 0.8805767297744751
Epoch 250/1500, Loss: 0.8552428483963013
Epoch 300/1500, Loss: 0.8381394147872925
Epoch 350/1500, Loss: 0.8256418704986572
Epoch 400/1500, Loss: 0.8157903552055359
Epoch 450/1500, Loss: 0.8073647022247314
Epoch 500/1500, Loss: 0.7996431589126587
Epoch 550/1500, Loss: 0.792230486869812
Epoch 600/1500, Loss: 0.7848939299583435
Epoch 650/1500, Loss: 0.7775012850761414
Epoch 700/1500, Loss: 0.7699931859970093
Epoch 750/1500, Loss: 0.7623674273490906
Epoch 800/1500, Loss: 0.7546666860580444
Epoch 850/1500, Loss: 0.7469660043716431
Epoch 900/1500, Loss: 0.7393587231636047
Epoch 950/1500, Loss: 0.7319421172142029
Epoch 1000/1500, Loss: 0.7248038053512573
Epoch 1050/1500, Loss: 0.7180129289627075
Epoch 1100/1500, Loss: 0.711614727973938
Epoch 1150/1500, Loss: 0.7056317925453186
Epoch 1200/1500, Loss: 0.7000667452812195
Epoch 1250/1500, Loss: 0.6949079632759094
Epoch 1300/1500, Loss: 0.6901333332061768
Epoch 1350/1500, Loss: 0.6857159733772278
Epoch 1400/1500, Loss: 0.6816268563270569
Epoch 1450/1500, Loss: 0.6778366565704346
Epoch 1500/1500, Loss: 0.6743176579475403Evaluamos la red neuronal.
Accuracy: 0.9666666666666667Esto mejora la precisión de la red neuronal. Podemos visualizar la matriz de confusión.
La inicialización de los pesos de la red neuronal puede afectar significativamente el rendimiento del modelo. En general, es importante inicializar los pesos de la red neuronal de manera que no se saturen las neuronas y se evite el problema del desvanecimiento o explosión del gradiente. Existen diversas técnicas de inicialización de pesos que se pueden utilizar para mejorar el rendimiento de la red neuronal artificial. Una de ellas es la inicialización de Xavier, que ajusta los pesos de la red neuronal de manera que la varianza de las salidas de las neuronas sea igual a la varianza de las entradas de las neuronas.
Otro aspecto importante es la regularización de la red neuronal, que se utiliza para evitar el sobreajuste de la red neuronal a los datos de entrenamiento. Existen diversas técnicas de regularización que se pueden utilizar para mejorar el rendimiento de la red neuronal artificial. Una de ellas es la regularización L2, que penaliza los pesos de la red neuronal para evitar que se vuelvan demasiado grandes.
Además, es importante ajustar los hiperparámetros de la red neuronal, como el número de capas ocultas, el número de neuronas en cada capa oculta, la tasa de aprendizaje, el número de épocas de entrenamiento, etc. para mejorar el rendimiento de la red neuronal artificial.
Es importante la escala de los datos, ya que si los datos no están normalizados, la red neuronal puede tener dificultades para converger. Por lo tanto, es importante normalizar los datos antes de entrenar la red neuronal artificial.
Existen diversas formas de normalizar los datos, como la normalización min-max, la normalización z-score, la normalización por rango, etc. En python, podemos utilizar la librería scikit-learn para normalizar los datos.
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import RobustScaler
# Normalizar los datos utilizando la normalización min-max
scaler = MinMaxScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
df = pd.DataFrame(X_train, columns=iris.feature_names)
print(df.head())
# Normalizar los datos utilizando la normalización z-score
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
df = pd.DataFrame(X_train, columns=iris.feature_names)
print(df.head())
# Normalizar los datos utilizando la normalización por rango
scaler = RobustScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
df = pd.DataFrame(X_train, columns=iris.feature_names)
print(df.head()) sepal length (cm) sepal width (cm) petal length (cm) petal width (cm)
0 0.250000 0.590909 0.084746 0.041667
1 0.583333 0.454545 0.593220 0.583333
2 0.472222 0.545455 0.593220 0.625000
3 0.500000 0.318182 0.627119 0.541667
4 0.388889 0.363636 0.542373 0.458333
sepal length (cm) sepal width (cm) petal length (cm) petal width (cm)
0 -0.813744 1.000766 -1.257121 -1.298710
1 0.611793 0.288759 0.384982 0.359218
2 0.136614 0.763431 0.384982 0.486751
3 0.255408 -0.423249 0.494455 0.231685
4 -0.219770 -0.185913 0.220772 -0.023381
sepal length (cm) sepal width (cm) petal length (cm) petal width (cm)
0 -0.461539 0.833333 -0.805369 -0.786885
1 0.461538 0.333333 0.000000 0.065574
2 0.153846 0.666667 0.000000 0.131148
3 0.230769 -0.166666 0.053691 0.000000
4 -0.076923 0.000000 -0.080537 -0.131147Es importante realizar este proceso después de haber dividido los datos en entrenamiento y prueba, para evitar el sesgo en la evaluación del modelo, ya que si se realiza antes de dividir los datos, se estaría utilizando información de la base de datos de prueba para normalizar los datos de entrenamiento y dar de forma indirecta información de la base de datos de prueba a la red neuronal.
TensorFlowTensorFlow es una librería de Python que permite implementar redes neuronales artificiales de manera eficiente. En particular, TensorFlow incluye una clase llamada tf.keras.Sequential que permite definir la arquitectura de la red neuronal artificial.
Para utilizar TensorFlow, primero debemos instalar la librería.
Tensorflow se basa igualmente en el uso de tensores para realizar operaciones matemáticas.
tf.Tensor(
[[0. 0. 0.]
[0. 0. 0.]], shape=(2, 3), dtype=float32)Podemos realizar operaciones matemáticas con tensores en TensorFlow.
# Crear dos tensores
x = tf.constant([[1, 2], [3, 4]], dtype=tf.float32)
y = tf.constant([[5, 6], [7, 8]], dtype=tf.float32)
# Sumar los tensores
z = x + y
print(z)
# Multiplicar los tensores
z = x * y
print(z)
# Multiplicar un tensor por un escalar
z = 2 * x
print(z)
# Calcular la transpuesta de un tensor
z = tf.transpose(x)tf.Tensor(
[[ 6. 8.]
[10. 12.]], shape=(2, 2), dtype=float32)
tf.Tensor(
[[ 5. 12.]
[21. 32.]], shape=(2, 2), dtype=float32)
tf.Tensor(
[[2. 4.]
[6. 8.]], shape=(2, 2), dtype=float32)Todo las operaciones que se pueden realizar en PyTorch se pueden realizar en TensorFlow.
Veamos las distintas partes de una red neuronal artificial en TensorFlow.
En este ejemplo, vamos a utilizar la base de datos iris para entrenar una red neuronal artificial que permita clasificar las flores en tres categorías: setosa, versicolor y virginica.
Model: "sequential_7"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ dense_21 (Dense) │ (None, 10) │ 50 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_22 (Dense) │ (None, 10) │ 110 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_23 (Dense) │ (None, 3) │ 33 │ └─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 193 (772.00 B)
Trainable params: 193 (772.00 B)
Non-trainable params: 0 (0.00 B)
Con TensorFlow se puede definir la red neuronal de manera más sencilla que con PyTorch. En este caso, utilizamos la clase tf.keras.Sequential para definir la arquitectura de la red neuronal artificial. La clase tf.keras.layers.Dense representa una capa de neuronas completamente conectada. En este caso, definimos tres capas de neuronas con 10, 10 y 3 neuronas respectivamente. La función tf.keras.Input define la capa de entrada de la red neuronal.
Vamos a entrenar la red neuronal.
import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
# Cargar la base de datos iris
iris = load_iris()
X = iris.data
y = iris.target
# Dividir la base de datos en entrenamiento y prueba
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1014)
# Convertir los datos a tensores de TensorFlow
X_train = tf.constant(X_train, dtype=tf.float32)
X_test = tf.constant(X_test, dtype=tf.float32)
y_train = tf.constant(y_train, dtype=tf.int64)
y_test = tf.constant(y_test, dtype=tf.int64)
print(X_train.shape)
print(X_test.shape)
print(y_train.shape)
print(y_test.shape)
# Compilar la red neuronal
model.compile(optimizer='sgd', loss='sparse_categorical_crossentropy', metrics=['accuracy'])
# Entrenar la red neuronal
model.fit(X_train, y_train, epochs=1000, verbose=0)
# Evaluar la red neuronal
loss, accuracy = model.evaluate(X_test, y_test)
print(f"Loss: {loss}, Accuracy: {accuracy}")(120, 4)
(30, 4)
(120,)
(30,)
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 98ms/step - accuracy: 1.0000 - loss: 0.03731/1 ━━━━━━━━━━━━━━━━━━━━ 0s 100ms/step - accuracy: 1.0000 - loss: 0.0373
Loss: 0.03730132058262825, Accuracy: 1.0Con el método compile se compila la red neuronal con un optimizador, una función de pérdida y métricas de evaluación. En este caso, utilizamos el optimizador sgd (descenso de gradiente estocástico), la función de pérdida sparse_categorical_crossentropy y la métrica accuracy para evaluar la precisión de la red neuronal.
Con el método fit se entrena la red neuronal con los datos de entrenamiento. En este caso, utilizamos 1000 épocas de entrenamiento. El argumento verbose=0 indica que no se mostrará información sobre el entrenamiento, para mostrar la información se puede cambiar a verbose=1.
Con el método evaluate se evalúa la red neuronal con los datos de prueba. El método evaluate devuelve la pérdida y la precisión de la red neuronal en los datos de prueba.
Podemos obtener las predicciones de la red neuronal para la base de datos de prueba.
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 35ms/step
[[9.3780188e-03 9.9053556e-01 8.6380802e-05]
[2.6691245e-05 6.1251414e-01 3.8745919e-01]
[2.8749557e-07 5.9596896e-02 9.4040269e-01]
[9.9821705e-01 1.7829464e-03 7.0882692e-12]
[3.1476901e-04 9.9696678e-01 2.7184207e-03]
[9.9806172e-01 1.9382917e-03 4.5069222e-12]
[4.7594633e-05 9.9566221e-01 4.2900806e-03]
[9.9946874e-01 5.3111481e-04 5.8261650e-14]
[7.6720468e-04 9.9874258e-01 4.9011409e-04]
[4.5947208e-06 3.0641466e-01 6.9358081e-01]
[9.9916506e-01 8.3498686e-04 3.6297191e-13]
[6.1792984e-05 9.9003565e-01 9.9024186e-03]
[9.9943411e-01 5.6587165e-04 6.9331653e-14]
[1.2681982e-04 9.9869889e-01 1.1743259e-03]
[1.3101969e-07 6.3623767e-03 9.9363756e-01]
[1.1187630e-03 9.9319637e-01 5.6849075e-03]
[9.9854863e-01 1.4513362e-03 3.3198364e-12]
[9.9968213e-01 3.1789864e-04 6.2396470e-15]
[2.2063234e-04 9.5556730e-01 4.4211969e-02]
[2.8410594e-03 9.9692291e-01 2.3596971e-04]
[2.3421185e-08 3.8140393e-03 9.9618596e-01]
[2.8064492e-04 9.9876738e-01 9.5207797e-04]
[2.1451027e-10 4.6397839e-04 9.9953604e-01]
[3.4913389e-04 9.9937332e-01 2.7746896e-04]
[9.9886537e-01 1.1346943e-03 1.2733420e-12]
[3.7266931e-04 9.9817073e-01 1.4565402e-03]
[1.1772375e-04 9.2994481e-01 6.9937520e-02]
[9.9625766e-01 3.7422990e-03 1.7923980e-10]
[2.0222605e-04 9.8535591e-01 1.4441739e-02]
[1.8129933e-09 2.6365283e-03 9.9736351e-01]]Para obtener la clase predicha, podemos usar la función argmax de NumPy.
[1 1 2 0 1 0 1 0 1 2 0 1 0 1 2 1 0 0 1 1 2 1 2 1 0 1 1 0 1 2]Podemos visualizar la matriz de confusión.
En PyTorch se pueden guardar y cargar modelos utilizando el método save y load.
En TensorFlow se pueden guardar y cargar modelos utilizando el método save y load.
Esto sirve para guardar el modelo y poder utilizarlo en otro momento sin tener que volver a entrenarlo.
En este tutorial, hemos visto cómo implementar redes neuronales artificiales en Python utilizando las librerías scikit-learn, PyTorch y TensorFlow. Hemos visto cómo cargar una base de datos, dividirla en entrenamiento y prueba, definir la arquitectura de la red neuronal, entrenar la red neuronal, evaluar la red neuronal y visualizar la matriz de confusión. También hemos visto cómo normalizar los datos y ajustar los hiperparámetros de la red neuronal para mejorar el rendimiento del modelo.
